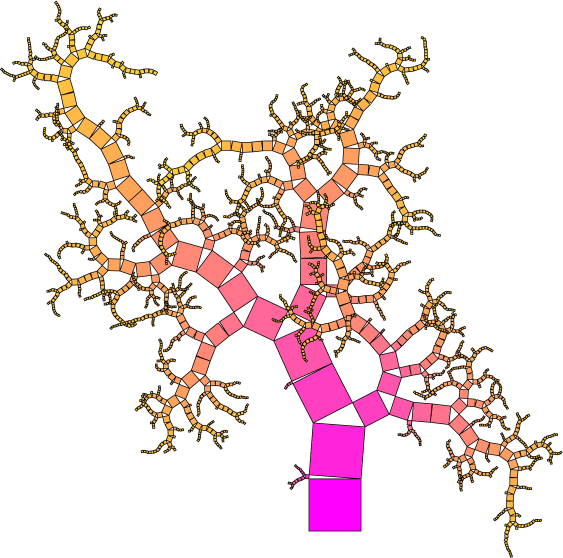
I took each random vertex uniformly on a halfcircle, but one could consider other distributions as well. Here are some theoretical questions related to it.
- Consider n generations of squares (2^n squares in the last level considered), choose one of these squares uniformly at random, and let X_n denote its location. What is the limit distribution of X_n as n tends to infinity? (Easy.)
- If I let each branch grow until its last square reaches area 1/n, then what is the path length of the longest branch (as a function of n)? (Hint: can you find a random binary search tree in there?)
- What is the limit law of the maximal distance from a square in generation n to the origin? (Hard.)
|
| ||
|
| |||
|
| ||
|
| |||
|
| ||
|
| |||
|
| ||
|
| |||
|
| ||
|
| |||
|
| ||
|
| |||
|
| ||
|
| |||
|
| ||
|
| |||
|
| ||
|
In the last three trees, I flipped triangles to make the largest branch always grow most vertically up. | |||
| Contact |
Luc Devroye |